[Solution] Path Prefixes Codeforces Solution

G. Path Prefixes

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a rooted tree. It contains n$n$ vertices, which are numbered from 1$1$ to n$n$. The root is the vertex 1$1$.

Each edge has two positive integer values. Thus, two positive integers aj$a_j$ and bj$b_j$ are given for each edge.

Output n−1$n-1$ numbers r2,r3,…,rn$r_2,r_3,\dots ,r_n$, where ri$r_i$ is defined as follows.

Consider the path from the root (vertex 1$1$) to i$i$ (2≤i≤n$2\le i\le n$). Let the sum of the costs of aj$a_j$ along this path be Ai$A_i$. Then ri$r_i$ is equal to the length of the maximum prefix of this path such that the sum of bj$b_j$ along this prefix does not exceed Ai$A_i$.

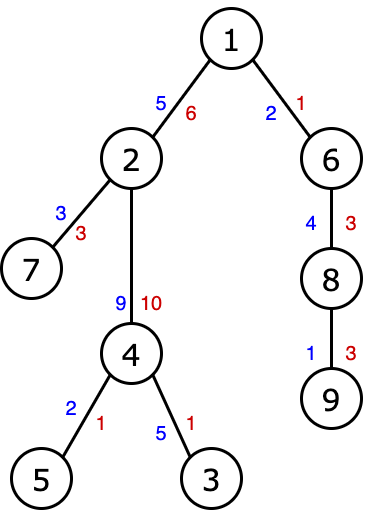Example for n=9$n=9$. The blue color shows the costs of aj$a_j$, and the red color shows the costs of bj$b_j$.

Consider an example. In this case:

• r2=0$r_2=0$, since the path to 2$2$ has an amount of aj$a_j$ equal to 5$5$, only the prefix of this path of length 0$0$ has a smaller or equal amount of bj$b_j$;
• r3=3$r_3=3$, since the path to 3$3$ has an amount

Solution Click Below:-  👉CLICK HERE👈

👇👇👇👇👇

 occupied

•  of aj$a_j$ equal to 5+9+5=19$5+9+5=19$, the prefix of length 3$3$ of this path has a sum of bj$b_j$ equal to 6+10+1=17$6+10+1=17$ ( the number is 17≤19$17\le 19$);
• r4=1$r_4=1$, since the path to 4$4$ has an amount of aj$a_j$ equal to 5+9=14$5+9=14$, the prefix of length 1$1$ of this path has an amount of bj$b_j$ equal to 6$6$ (this is the longest suitable prefix, since the prefix of length 2$2$ already has an amount of bj$b_j$ equal to 6+10=16$6+10=16$, which is more than 14$14$);
• r5=2$r_5=2$, since the path to 5$5$ has an amount of aj$a_j$ equal to 5+9+2=16$5+9+2=16$, the prefix of length 2$2$ of this path has a sum of bj$b_j$ equal to 6+10=16$6+10=16$ (this is the longest suitable prefix, since the prefix of length 3$3$ already has an amount of bj$b_j$ equal to 6+10+1=17$6+10+1=17$, what is more than 16$16$);
• r6=1$r_6=1$, since the path up to 6$6$ has an amount of aj$a_j$ equal to 2$2$, the prefix of length 1$1$ of this path has an amount of bj$b_j$ equal to 1$1$;
• r7=1$r_7=1$, since the path to 7$7$ has an amount of aj$a_j$ equal to 5+3=8$5+3=8$, the prefix of length 1$1$ of this path has an amount of bj$b_j$ equal to 6$6$ (this is the longest suitable prefix, since the prefix of length 2$2$ already has an amount of bj$b_j$ equal to 6+3=9$6+3=9$, which is more than 8$8$);
• r8=2$r_8=2$, since the path up to 8$8$ has an amount of aj$a_j$ equal to 2+4=6$2+4=6$, the prefix of length 2$2$ of this path has an amount of bj$b_j$ equal to 1+3=4$1+3=4$;
• r9=3$r_9=3$, since the path to 9$9$ has an amount of aj$a_j$ equal to 2+4+1=7$2+4+1=7$, the prefix of length 3$3$ of this path has a sum of bj$b_j$ equal to 1+3+3=7$1+3+3=7$.

Input

The first line contains an integer t$t$ (1≤t≤104$1\le t\le {10}^4$) — the number of test cases in the test.

The descriptions of test cases follow.

Each description begins with a line that contains an integer n$n$ (2≤n≤2⋅105$2\le n\le 2\cdot {10}^5$) — the number of vertices in the tree.

This is followed by n−1$n-1$ string, each of which contains three numbers pj,aj,bj$p_j,a_j,b_j$ (1≤pj≤n$1\le p_j\le n$; 1≤aj,bj≤109$1\le a_j,b_j\le {10}^9$) — the ancestor of the vertex j$j$, the first and second values an edge that leads from pj$p_j$ to j$j$. The value of j$j$ runs through all values from 2$2$ to n$n$ inclusive. It is guaranteed that each set of input data has a correct hanged tree with a root at the vertex 1$1$.

It is guaranteed that the sum of n$n$ over all input test cases does not exceed 2⋅105$2\cdot {10}^5$.

Output

For each test case, output n−1$n-1$ integer in one line: r2,r3,…,rn$r_2,r_3,\dots ,r_n$.