White-Black Balanced Subtrees Codeforces Solution | Codeforces Problem Solution 2022

White-Black Balanced Subtrees Codeforces Solution | Codeforces Problem Solution 2022

G. White-Black Balanced Subtrees

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a rooted tree consisting of 𝑛$n$ vertices numbered from 1$1$ to 𝑛$n$. The root is vertex 1$1$. There is also a string 𝑠$s$ denoting the color of each vertex: if 𝑠𝑖=𝙱$s_i=\mathtt{\text{B}}$, then vertex 𝑖$i$ is black, and if 𝑠𝑖=𝚆$s_i=\mathtt{\text{W}}$, then vertex 𝑖$i$ is white.

A subtree of the tree is called balanced if the number of white vertices equals the number of black vertices. Count the number of balanced subtrees.

A tree is a connected undirected graph without cycles. A rooted tree is a tree with a selected vertex, which is called the root. In this problem, all trees have root 1$1$.

The tree is specified by an array of parents 𝑎2,…,𝑎𝑛$a_2,\dots ,a_n$ containing 𝑛−1$n-1$ numbers: 𝑎𝑖$a_i$ is the parent of the vertex with the number 𝑖$i$ for all 𝑖=2,…,𝑛$i=2,\dots ,n$. The parent of a vertex 𝑢$u$ is a vertex that is the next vertex on a simple path from 𝑢$u$ to the root.

Solution Click Below:-  CLICK HERE

The subtree of a vertex 𝑢$u$ is the set of all vertices that pass through 𝑢$u$ on a simple path to the root. For example, in the picture below, 7$7$ is in the subtree of 3$3$ because the simple path 7→5→3→1$7\to 5\to 3\to 1$ passes through 3$3$. Note that a vertex is included in its subtree, and the subtree of the root is the entire tree.

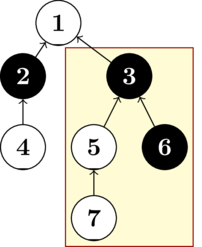The picture shows the tree for 𝑛=7$n=7$, 𝑎=[1,1,2,3,3,5]$a=[1,1,2,3,3,5]$, and 𝑠=𝚆𝙱𝙱𝚆𝚆𝙱𝚆$s=\mathtt{\text{WBBWWBW}}$. The subtree at the vertex 3$3$ is balanced.

Input

The first line of input contains an integer 𝑡$t$ (1≤𝑡≤104$1\le t\le {10}^4$) — the number of test cases.

The first line of each test case contains an integer 𝑛$n$ (2≤𝑛≤4000$2\le n\le 4000$) — the number of vertices in the tree.

The second line of each test case contains 𝑛−1$n-1$ integers 𝑎2,…,𝑎𝑛$a_2,\dots ,a_n$ (1≤𝑎𝑖<𝑖$1\le a_i<i$) — the parents of the vertices 2,…,𝑛$2,\dots ,n$.

The third line of each test case contains a string 𝑠$s$ of length 𝑛$n$ consisting of the characters 𝙱$\mathtt{\text{B}}$ and 𝚆$\mathtt{\text{W}}$ — the coloring of the tree.

Lucky? Codeforces Solution

Equal Candies Codeforces Solution

Most Similar Words Codeforces Solution

X-Sum Codeforces Solution

Eating Queries Codeforces Solution

Longest Strike Codeforces Solution

White-Black Balanced Subtrees Codeforces Solution

Maximum Crossings (Easy Version) Codeforces Solution

Maximum Crossings (Hard Version) Codeforces Solution

It is guaranteed that the sum of the values 𝑛$n$ over all test cases does not exceed 2⋅105$2\cdot {10}^5$.

Output

For each test case, output a single integer — the number of balanced subtrees.

Join Now for Solution:-